Количество ячеек соответствующих одному из значений

Например, у нас есть некий набор значений, и стоит задача посчитать, сколько ячеек из другого набора данных, соответствует какому либо исходному значению. То есть, есть список уникальных элементов «А», есть список элементов «Б» в котором есть значения из списка «А», причём значения могут быть не все, могут повторяться, могут быть значения которые и не входят в список «А», и необходимо посчитать количество ячеек соответствующих одному из значений списка «А».

Исходные данные

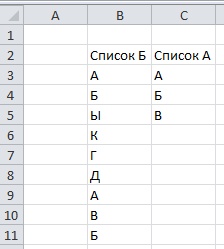
Пусть будут такие, простые, привычные данные. Разместили их для наглядности в обратном порядке. Итак, в списке «Б» все варианты, и повторяющиеся данные и лишние, да может быть еще что угодно. Список «А» у нас искомый, по нему будем считать количество ячеек в списке «Б».

Формула

Запишем в ячейке D3 следующую формулу:

=СУММПРОИЗВ(СЧЁТЕСЛИ(B3:B11;C3:C5))

Что же такое происходит. Всё очень просто функция «СЧЁТЕСЛИ» подсчитывает количество элементов соответствующих критерию в определенном диапазоне. Однако критерием для данной функции является определенное значение, а не диапазон значений. По этому если мы запишем в ячейке D3 формулу =СЧЁТЕСЛИ(B3:B11;C3:C5) получим результат 2. То есть в диапазоне В3:В11 будет подсчитано количество только одного критерия – буквы «А». Если напишем эту же формулу в ячейке D4, тоже получим значение – 2, а вот если эту формулу записать в ячейке D5  значение будет равно 1. Именно потому что берется в расчет критерия только одно значение, для ячейки D4 – буква Б, для ячейки D5 – буква В.

Хотя…если разобраться более точнее, то при указании в критерии указан диапазон, результатом функции «СЧЁТЕСЛИ» будет массив, просто массив вычисляется позиционно, относительно текущего индекса. При этом результат выполнения представляется в виде 0 и 1, если искомое значение найдено в диапазоне ставится в соответствующей позиции значение 1, иначе 0. Своего рода это эквивалент логического «ИСТИНА», «ЛОЖЬ».

Если бы у нас стояла задача посчитать количество вхождений в диапазон каждого элемента, мы бы обошлись только функцией «СЧЁТЕСЛИ», но у нас в задаче посчитать в одной формуле количество вхождений каждого элемента искомого списка. Именно поэтому мы используем дополнительно функцию «СУММПРОИЗВ». Может возникнуть вопрос, а почему не просто функцию «СУММ», в принципе можно, но функция «СУММ» хорошо работает с определенным набором элементов, те с ограниченным, а с диапазонами лучше работает «СУММПРОИЗВ».

ИТОГ

Итак, для решения задачи мы использовали особенность работы функции «СЧЁТЕСЛИ», которая возвращает массив, если в качестве критерия передается диапазон значений. Функцией «СУММПРОИЗВ» мы объединяем эти массивы и суммируем количество найденных элементов.